Intro to Transformers (Part 1) - Embeddings

I recently had an interview for a machine learning position and was asked a lot about the transformer architecture for my project. I realized that at the time of doing the project, I believed that I understood how the architecture worked; however, through the interview I realized that my understanding of the details on how it actually worked might have been not as deep as I expected. So this is the review that I needed and hopefully a review that can help others if they need a better understanding of the architecture. I am going to go through my project specifically, and try to provide code, and good explainations along the way.

Project: Chord generation through Transformers

So the objective that we want to achieve here is to train a model that can generate the next sequence of chords. You can think of the sequence of chords as a sequence of words, so a sentence: each chord represents a unique sound(word) and we want to use previous data of sequences to train our model to output new sequences.

Why can’t we use One-Hot Encoding?

First, there needs to be a way to represent our chords in a format that the model can interpret. One-hot encoding could be an option but given that there are a lot of chords, representing them as one-hot encodings may be inefficient as it means that in the input layer, there will be as many weights as there are the number of chords.

Furthermore, similiar chords, such as a C and a CM7 should represent similar sounds(meanings), which is a relationship that one-hot encodings cannot capture. These are all pitfalls of sparse data representations and will instead try to utilize embeddings to represent our chords.

Intro to Embeddings

So, what are embeddings? Embeddings are basically projecting the data to a lower dimensional space. So in the case of chords, assuming that there are 5000 chords in total, we want to represent these chords in say, a dimension of 512. This explanation isn’t too intuitive and I think the way I like to think about it is to trying group similar songs into genres.

For example, there are probably millions of songs available in the world, and say you want to represent these songs as numbers. The one-hot encoded way of achieving this is to assign a number for each of these songs. This is not what we want to do.

Instead we know that similiar songs can be grouped together. This might be controversial but a song from Oasis can be similar to a song from Blur because they both fit in the 90s/00s Rock genre. We can also group songs by, say the country of origin. By using the genre and country of origin, we can successfully represent each of the millions of songs into a vector of size 2, assuming that there are only a limited amount of genres and countries in the world.

So for our project, we want to somehow capture what the chords sounds into vectors, and want to have similar sounds to be closer to one another and have different sounds to be further away from one another in this embedding space. But how do we do that?

I’ll focus more on words here but will come back to the idea of chords because they are basically very similiar in terms of the context.

Static Embeddings(Word2Vec)

In Word2Vec, we learn word vector representations by training them to predict context words. The main idea is:

Start with random word vectors and have a sliding window with a central word(v).
Given surrounding words(u), compute probabilities with respect to the central word(v).
Increase the probability of actual surrounding words(u) given the central word(v).
repeat.

Why do we want to increase the probability of the surrounding words? Because words that are frequently together are likely to be semantically related (e.g Apple Juice: You make Juice with Apples and Apples can be made to Juice). By training words on surrounding words, we can make sure that similiar words are closer to one another, as the goal of our project.

I know that this still might sound vague and confusing so I found this diagram from Lena Voita that is very helpful.

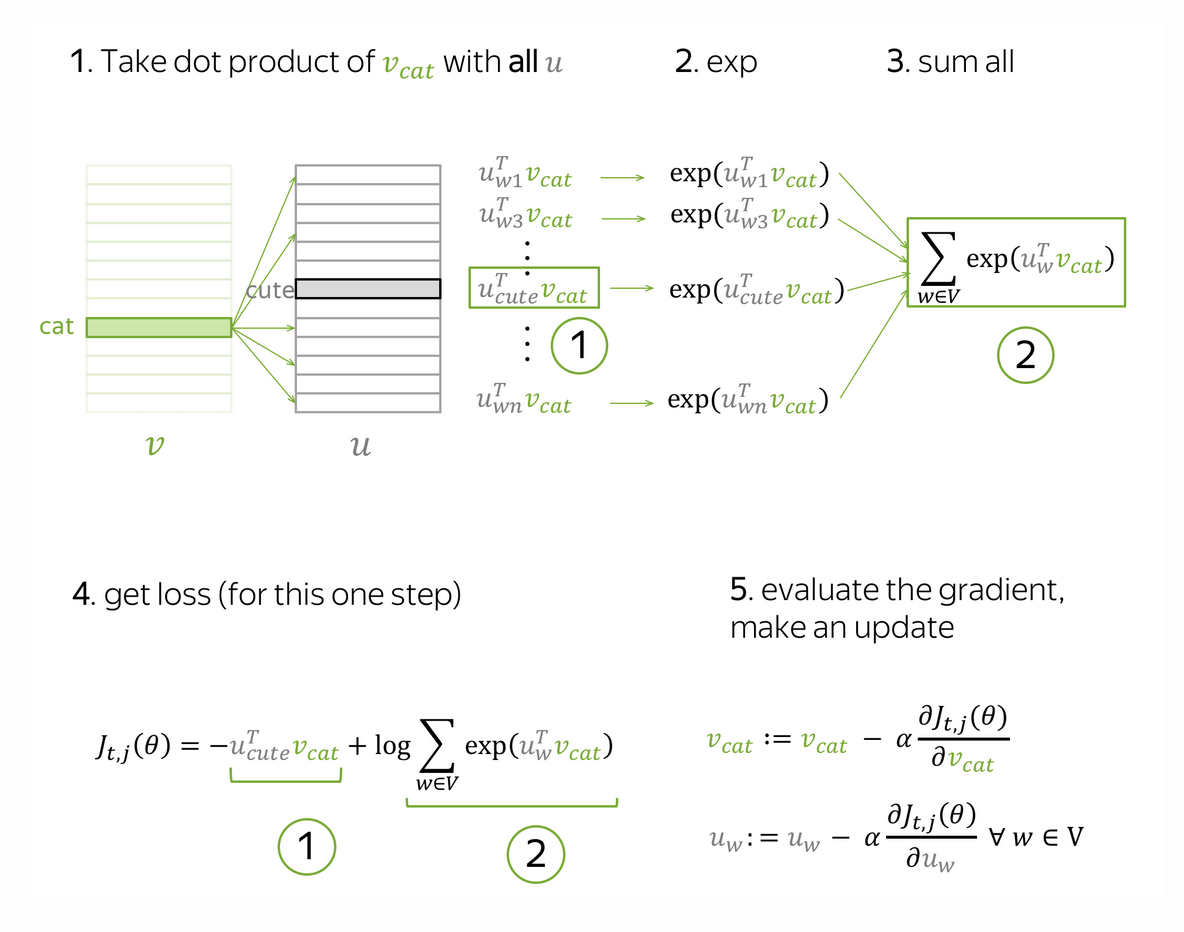
Schematic Illustration of Word2Vec (Lena Voita)

For this example, the sentance is: “cute grey cat playing in”.

Given the central word “cat”, first we compute the dot product(represents similarity between the two words) for its surrounding words(u).
Here step 4. is equivalent to writing the softmax for ths specific pair of “cat” and “cute”, which represents the negative likelihood of obtaining the word “cute” given the central word “cat”.
At step 5, we then use this to evaluate this loss and update our gradients to our corresponding parameters, which in this case are simply the vectors of the words itself.

There are a couple of points that I want to touch upon here and the first is negative log likelihood. Where does this come up?

If you recall, from the beginning, we want to maximize the probability of observing the context words given the central word. This is a Maximum Likelihood problem, where we aim to maximize the product of the probabilities of the context word given the central word in a sliding window.

However, with respect to training ML models, we tend to minimize a loss rather than to maximize a function. This is where we usually see maximization functions converted to minimizing a negative function. The log is usually added for numerical stability for training as when we’re calculating gradients, log functions are smoother and thus, gives better updates to our weights.

The second part is: how are the conditional probabilities calculated? For this part, we use the softmax function, which represents logits(raw numbers) into normalized probabilites(sums upto 1). So for this case, it represents the probability of the pair cat and cute given all the probabilities of different pairs the word cat can go with.

Potential Issues with Static Embeddings

One of the issues with Static Embeddings is that once it has been trained, it isn’t really updated as we introduce new data. For example, if in our corpus that we trained our embeddings only had examples of “Apple Juice” and no “Apple Pie”, The word “Apple” will always be closer to the embeddings of “Juice”, “Soda” .. etc. To mitigate this limitation, we introduce Learned Embeddings.

Learned Embeddings

So in order to make sure that we are in fact taking account of more rich representations of text, we can actually have an embedding layer to learn embeddings through training. I’ll first share the code use for this embedding layer first and try to explain it line by line.

class InputEmbedding(nn.Module):
    def __init__(self, vocab_size, d_model):
        super(InputEmbedding, self).__init__()
        self.embedding = nn.Embedding(vocab_size, d_model)

    def forward(self, x):
        return self.embedding(x) * math.sqrt(self.embedding.embedding_dim)

For this embedding layer, we first make use of nn.Embedding(vocab_size, d_model), which is simply a \(M \times N\) matrix, with \(M\) being the dimensions of the number of unique chords(words) in the input and \(N\) being the size of the embedding. So this layer initializes our embedding matrix for our inputs of chords.

So what does the input to this layer look like? It looks something like: (batch_size, sequence_length). I’ll get more into batching in a later post but for now, keep in mind that the \(x\) will look something like:

x = [
  [1,20,31],
  [19,8,111],
  ...
]

, where each number in this tensor represents the index in the dictionary of the vocabulary. So for example, my dictionary of chords are: {1: 'Cmaj', 2:'Cm7' ... 20: 'E', .. 31: 'Fm'...} and we have a sequence of chords of ['Cmaj', 'Fm', 'E', 'Cm7'], we would use something like a dictionary to tranform it into [1, 31, 20, 2] for our input for our embedding layer.

So now, knowing that our input tensor is the shape of (batch_size, sequence_length), once it passes the embedding layer, it will return (batch_size, sequence_length, embedding_dim). In other words, it retrieves the corresponding embedding for each of the chords (For those who have the question of: “What if the sequence lengths are different for different progressions in a batch?”, I’ll address it in the batching part of the series but for now, you can assume that they are all equal).

Now, the last step is multiplying math.sqrt(self.embedding.embedding_dim). This comes directly from the transformer paper and it is for numerical stability when training as the embeddings, as they are randomly initialized to a small number so we want to scale the values in order to have stable gradients.

However, this is something that I’m not 100% sure if it is based on some theory; to me it seems like a more heuristic to improve on the training of the model so I would not worry too much about it. Thanks for reading so far, the next post will be on positional encoding!

Sources: