Softmax with Temperature

Temperature and SoftMax

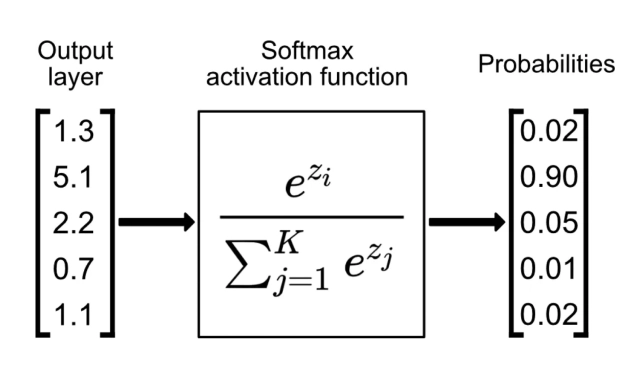
So if you remember the softmax function, it transforms logits(raw values) to normalized probabilities as it is the exponential over the sum of all the logits. So what is temperature and where does it come into place?

Let’s look at the softmax with temperature below.

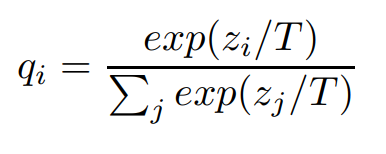
So temperature divides each of the terms by \(T\). What does this exactly do? First, we have to consider the edge cases. So when temperature is close to 0, the \(z_{i}\) term goes to \(\infty\), which means \(e^{z_{i}} \to \infty\) for each \(z_{i}\). So it’s just all \(\infty / \infty\)?? Not quite because it is important to recognize each of the \(e^{z_{i}}\) gets larger at different speeds.

To visualize this, I plotted \(e^{z_{i}/K}\) and \(x=[1,3,10]\). The first gif shows what happens when I decrease the value of K closer to 0. You can see that in the end, all \(x\) values do reach \(\infty\); however, they reach there at different speeds. Therefore, larger values will become larger faster while smaller values will get there slower - So higher logits will get more higher and smaller logits will stay smaller. This suggests that decreasing temperature can make the distribution more deterministic and results in less randomness.

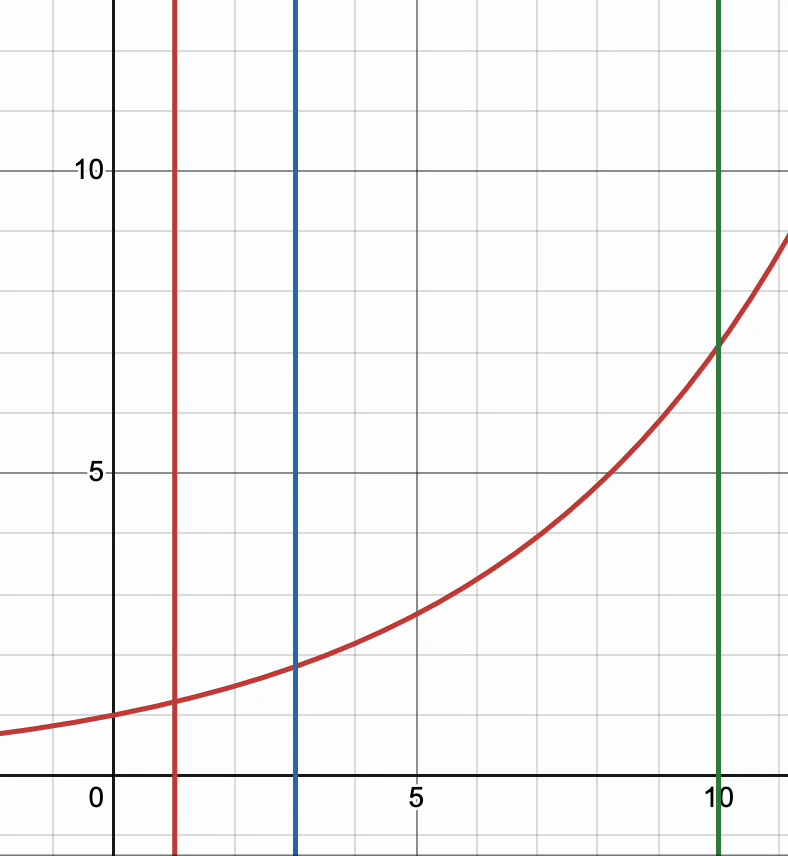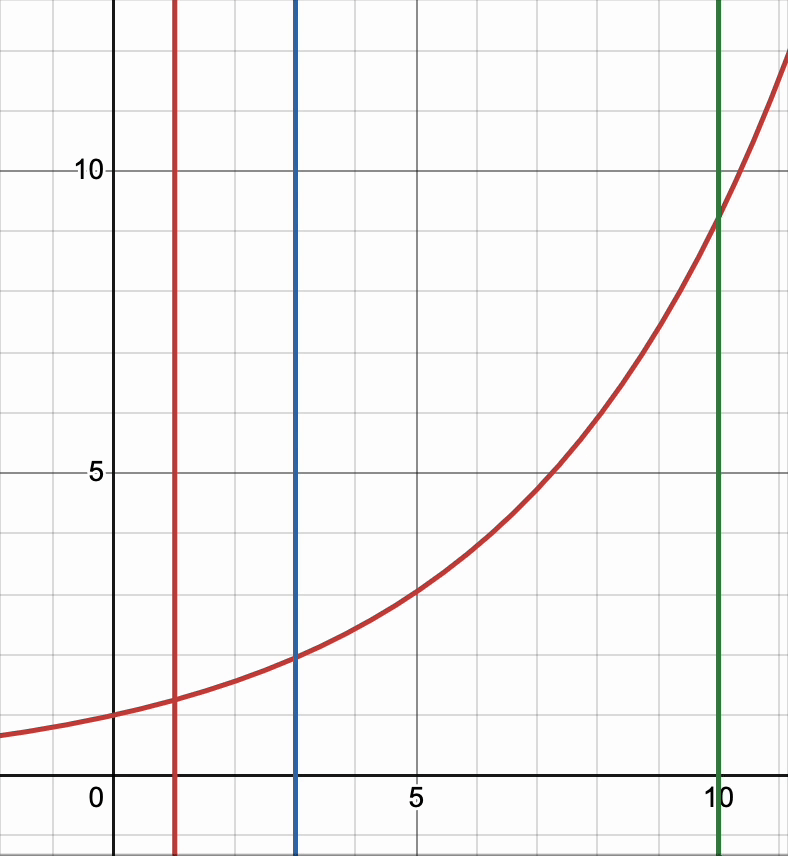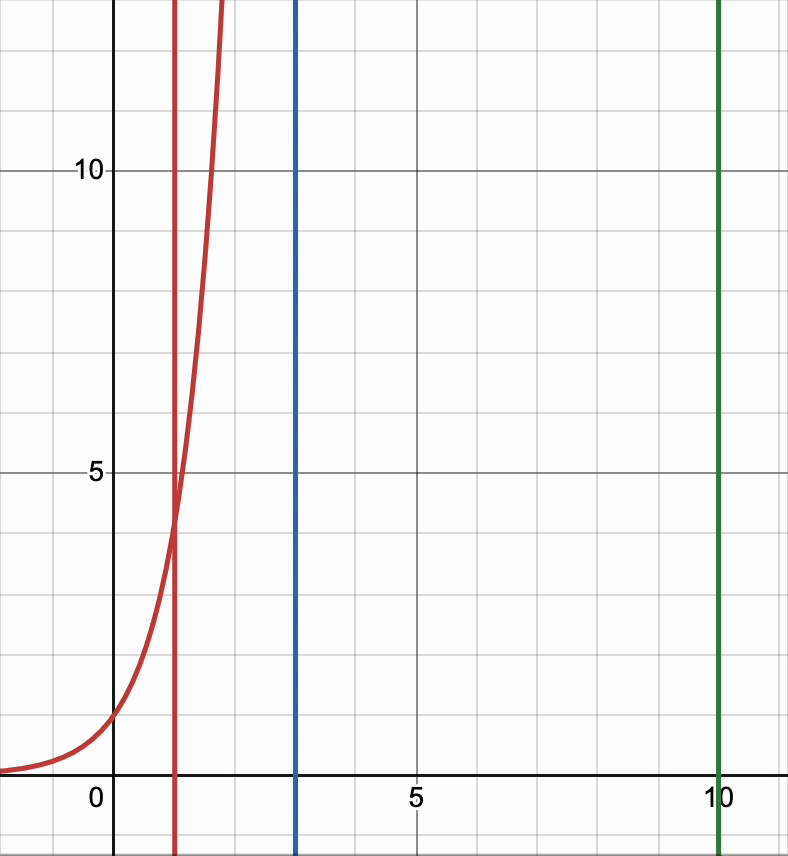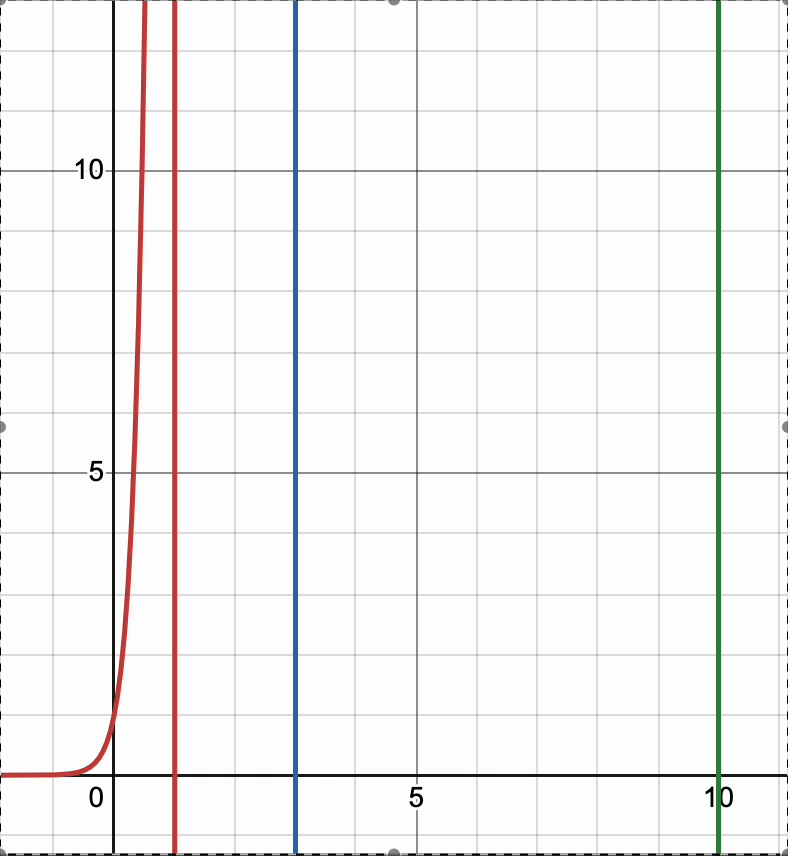
On the other hand, if we increase K to be a large number, we can see that each of the values eventually reach to \(1\), which aligns with our intutition that \(e^{0} \to 1\). This suggests that increasing temperature can lead to increased randomness and higher stochasticity when sampling from this distribution.

Hope this is an intuitive way to visualize how temperature may affect the randomness when sampling from a softmax probability distribution.